Ортоцентр что такое: Свойства высот треугольника. Ортоцентр – подготовка к ЕГЭ по Математике – Значение слова ОРТОЦЕНТР. Что такое ОРТОЦЕНТР?

Содержание

Свойства высот треугольника. Ортоцентр – подготовка к ЕГЭ по Математике

Анна Малкова

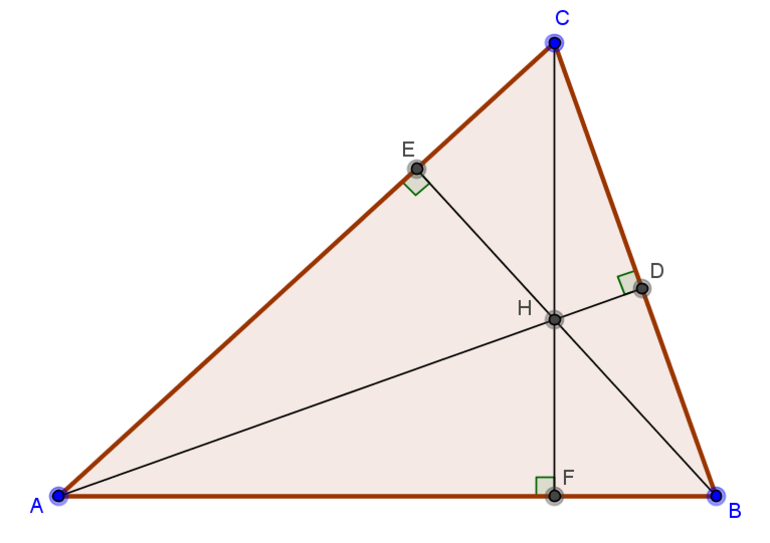
Схема 1. В треугольнике АВС проведены высоты АМ и СК.
Н – точка пересечения высот треугольника (ортоцентр), Н=АМ∩СК

Запомните этот рисунок. Перед вами – схема, из которой можно получить сразу несколько полезных фактов.

1. Треугольники МВК и △АВС, подобны, причем коэффициент подобия
, если k=cosB , и k=cosB , если k=cosB

Четырехугольник АКМС можно вписать в окружность. Эта вспомогательная окружность поможет решить множество задач.
Четырехугольник ВКМН также можно вписать в окружность.
Радиусы окружностей, описанных вокруг треугольников АВС, АНС, ВНС и АВН, равны.

,где R – радиус описанной окружности .

Докажем эти факты по порядку.

1) Заметим, что на рисунке есть подобные треугольники. Это АВМ и СВК, прямоугольные треугольники с общим углом В, и они подобны по двум углам

Мы получили, что в треугольниках МВК и АВС стороны, прилежащие к углу В, пропорциональны. Получаем, что по углу и двум сторонам.

2) Докажем, что вокруг четырехугольника АКМС можно описать окружность. Для этого необходимо и достаточно, чтобы суммы противоположных углов четырехугольника АКМС были равны .

Пусть ∠ACB=∠BKM=γ (поскольку треугольники МВК и АВС подобны), тогда
– как смежный с углом ВКМ. Получили, что , и это значит, что четырехугольник AKMC можно вписать в окружность.

3) Рассмотрим четырехугольник KBMH. Его противоположные углы ВКН и ВМН – прямые, их сумма равна , и значит, четырехугольник КВМН можно вписать в окружность.

4) По теореме синусов, радиус окружности, описанной вокруг треугольника АВС,

Радиус окружности, описанной вокруг треугольника АНС,
Мы помним, что . Значит, синусы углов АВС и АНС равны, и радиусы окружностей, описанных вокруг треугольников АВС и АНС равны.

5) Докажем, что ,где R – радиус описанной окружности . Поскольку четырехугольник КВМН можно вписать в окружность и углы ВКН и ВМН – прямые, отрезок ВН является диаметром этой окружности. Треугольник МВК также вписан в эту окружность, и по теореме синусов, .

Диаметр окружности, описанной вокруг треугольника АВС, равен Поскольку треугольники МВК и АВС подобны, отношение диаметров описанных вокруг них окружностей равно . Получили, что

Задача ЕГЭ по теме «Высоты треугольника» (Профильный уровень, №16)

2. В остроугольном треугольнике KMN проведены высоты KB и NA.

а) Докажите, что угол ABK равен углу ANK.

б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и

$\angle KMN=45{^\circ }$

а) Докажем, что
(по двум углам). Запишем отношение сходственных сторон:
Но это значит, что (по углу и двум сторонам), причем .

– смежный с углом ,
,
,четырехугольник ABNK можно вписать в окружность.
(опираются на одну дугу).

б) Найдем , если и

По теореме синусов,

ортоцентр – это… Что такое ортоцентр?

ортоцентр — ортоцентр … Орфографический словарь-справочник

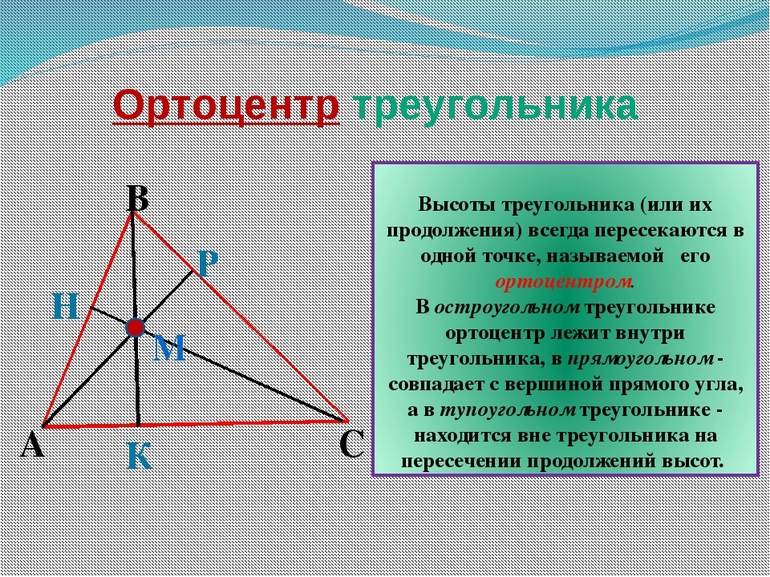
Ортоцентр — (от греч. ορθοξ прямой) точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависим … Википедия

ОРТОЦЕНТР — (от греч. orthos прямой правильный и центр), точка пересечения трех высот треугольника … Большой Энциклопедический словарь

ОРТОЦЕНТР — ОРТОЦЕНТР, ортоцентра, муж. (от греч. orthos правильный и лат. centrum центр) (мат.). Точка пересечения трех высот треугольника. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ортоцентр — сущ., кол во синонимов: 1 • точка (100) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

Ортоцентр — (от греч. orthós прямой, правильный и лат. centrum центр) точка пересечения трёх высот треугольника (см. рис.). Во всяком треугольнике точка пересечения медиан, центр описанного круга и О. лежат на одной прямой. Рис. к ст … Большая советская энциклопедия

ортоцентр — (от греч. orthós прямой, правильный и центр), точка пересечения трёх высот треугольника. * * * ОРТОЦЕНТР ОРТОЦЕНТР (от греч. orthos прямой, правильный и центр (см. ЦЕНТР (в математике))), точка пересечения трех высот треугольника … Энциклопедический словарь

ортоцентр — ортоцентр, ортоцентры, ортоцентра, ортоцентров, ортоцентру, ортоцентрам, ортоцентр, ортоцентры, ортоцентром, ортоцентрами, ортоцентре, ортоцентрах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов

ОРТОЦЕНТР — треугольника точка пересечения трех высот треугольника. О. треугольника лежит на Эйлера прямой. Середины трех сторон, середины отрезков, соединяющих О. с тремя вершинами, и основания высот треугольника лежат на одной окружности. О. является… … Математическая энциклопедия

ОРТОЦЕНТР — (от греч. orthоs прямой, правильный и центр), точка пересечения трёх высот треугольника … Естествознание. Энциклопедический словарь

Точка пересечения высот треугольника ℹ️ определение, свойства, расположение и координаты ортоцентра, доказательство теоремы, нахождение точки

Что такое высота

Если из вершины опустить перпендикуляр на противоположную сторону, получится отрезок, который именуется высотой. В равнобедренном треугольнике 2 отрезка равны, а в равностороннем равны все 3.

У фигур с углами 90 и более градусов высота попадает на противоположную сторону. В случае острого угла дело обстоит иначе. Прямая попадет только на продолжение противоположной стороны и будет находиться вне самой фигуры. Таким образом, если все углы острые, отрезки будут находиться внутри, как и ортоцентр. В тупоугольной фигуре два из трех отрезков будут проходить за его пределами — ортоцентр окажется вне фигуры.

Свойства ортоцентра

Свойства высот треугольника, пересекающихся в одной точке, давно изучены и описаны. Согласно основному из них, все 3 высоты всегда пересекаются в одном месте. Иногда, чтобы найти это место, отрезки нужно продлить, превратив в ортогональные прямые.

Ортоцентр по отношению к фигуре может быть расположен:

внутри;
снаружи;
в вершине (у прямоугольных треугольников)

Ортоцентр — важная в геометрии характеристика, влияющая на нахождение золотого сечения.

Так называется маленький треугольник, расположенный внутри основного, находящийся на пересечении его трех параметров:

биссектрис,
высот,
медиан.

Золотое сечение может представлять собой не только треугольную фигуру, но и отрезок. В правильном треугольнике медианы, биссектрисы и высоты совпадают, значит, золотое сечение превращается в точку.

Полезные факты

Местонахождение ортоцентра имеет некоторые закономерности. Их знание принесет пользу при решении задач.

Пусть:

H — ортоцентр в ABC;
О — центр описанной окружности.

Тогда:

окружности, описанные вокруг АБС, АНВ, CHB, HCA, равны:
отрезок BH вдвое длиннее отрезка АС;
середины отрезков AC и BH разделены расстоянием, равным радиусу описанной окружности.

Задача Фаньяно

Это классическая теорема. Она возникла в процессе поиска фигур с наименьшим периметром. Теорему доказал Фаньяно — итальянский математик и инженер. Это произошло еще в начале XVIII века.

Формулировка: ортотреугольник, то есть фигура, полученная соединением трех оснований треугольника, проведенный внутри остроугольного треугольника, имеет самый маленький периметр изо всех возможных, вписанных в данную фигуру.

Площадь ортотреугольника рассчитывается по формуле:

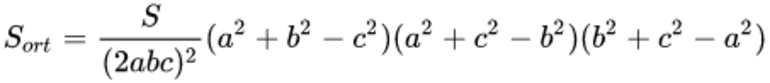
Здесь S — площадь, а, b, c — стороны.

Существует понятие ортоцентрической системы. Оно включает в себя 3 вершины и место пересечения их высот. Любая из данных четырех точек будет являться ортоцентром треугольника, образованного тремя остальными.

История изучения

Важное значение имеет место пересечения медиан или центр тяжести. Вместе с ортоцентром это еще одна «замечательная точка», которая была известна еще древним грекам. Так их стали называть начиная с 18 века, другое название «особенные».

Исследование этих точек стало началом для создания геометрии треугольника, основателем которой считается Леонард Эйлер. Ученый показал, что в любом треугольнике точки соединения высот, медиан и центр описанного круга находятся на одной линии, которую позже назвали прямой Эйлера.

В позапрошлом веке была обнаружена окружность 9 точек или Фейербаха. Она состоит из оснований медиан, высот и центров высот. Оказалось, что все эти точки лежат на общей окружности, центр которой находится на линии Эйлера.

Каждый отрезок, прочерченный из ортоцентра до соединения с описанной окружностью, всегда будет делиться линией Эйлера на 2 равные части.

Треугольник — удивительная фигура, изучением которой занимается целый раздел геометрии. Ортоцентр и его свойства имеют широкое применение в практической жизни, например, в строительстве. Этот показатель настолько важен и распространен, что существуют калькуляторы, позволяющие определить местонахождение точки по координатам вершин.

Ортоцентр треугольника. Ортотреугольник. Свойства ортоцентра треугольника

Ортоцентр — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).

Свойства

Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.

Радиусы окружностей проходящих через любые три точки ортоцентрической системы равны.

Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).

Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.

Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.

Точки, симметричные ортоцентру относительно его сторон, лежат на описанной окружности.

Точки, симметричные ортоцентру относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.

Если О — центр описанной окружности ΔABC, то .

Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.

Ортотреуго́льник (ортоцентрический треугольник) треугольника ∆ABC — треугольник, вершины которого являются основаниями высот ∆ABC.

Свойства

1. . Ортоцентрический треугольник остроугольного треугольника АВС обладает наименьшим периметром из всех вписанных треугольников.

2. Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).

3. Если точки A₁, B₁ и C₁ на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что

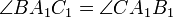то A₁B₁C₁ — ортотреугольник треугольника ABC.

4. Точки касания вписанной в данный треугольник окружности соединены отрезками, и в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника.

Ортотреугольник отсекает треугольники, подобные данному.
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.

7. Высоты треугольника являются биссектрисами ортотреугольника.

8. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .

9. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.

Про медиану и биссектрису в треугольнике в рамках школьной математике имеется много различных теорем, но вот про некоторые свойств высот умалчивается. Факт про незнание школьниками свойств высот, как мне кажется, активно используется при организации различных математических олимпиад и конкурсов. Т.е. такими задачами отсекаются сразу школьники, которые не занимаются математикой дополнительно.

Про высоты в треугольнике известно, что они проводятся перпендикулярно к сторонам, что точка пересечения срединных перпендикуляров является центром описанной окружности. Ну еще, что в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой. По моему, я перечислил все факты, что знают школьники о высотах.

Важной точкой является ортоцентр – точка пересечения высот. Известны следующие свойства ортоцентра:

Если точка H является ортоцентром треугольника ABC, то любая вершина является ортоцентром треугольника, составленного из остальных вершин, т.е. А – ортоцентр треугольника BCH и т.д. Точки A, B, C, H при этом называют ортоцентрической системой.
Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны.
Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.

Пусть O является центром описанной около треугольника ABC окружности, тогда дополнительно верны следующие утверждения:

.
. Здесь R – радиус описанной окружности.
Расстояние от вершины треугольника до ортоцентра вдвое больше расстояния от центра описанной окружности до противоположной стороны.

Здесь приведены наиболее используемые факты, связанные с перпендикулярами. Я настоятельно рекомендую запомнить эти свойства. А еще полезней будет провести доказательство этих утверждений, т.к. поняв доказательство, можно легко запомнить свойства.