Что такое ортоцентр – «Какие четыре точки называют “замечательными точками” треугольника?» – Яндекс.Знатоки
Ортоцентр — Википедия
Материал из Википедии — свободной энциклопедии
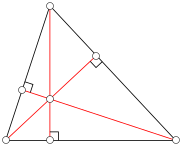
Ортоцентр (от др.-греч. ὀρθός «прямой») — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H{\displaystyle H}. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольном), вне его (в тупоугольном) или совпадать с вершиной (в прямоугольном — совпадает с вершиной при прямом угле). Ортоцентр относятся к замечательным точкам треугольника и перечислен в энциклопедии центров треугольника Кларка Кимберлинга как точка X(4).
- Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют
- Более того, при любом разбиении множества ортоцентрической системы точек {A, B, C, D} на две пары, например, {B, C} и {A, D} или при любом другом подобном разбиении, всегда перпендикулярны образующиеся два отрезка прямых с концами в данных точках множеств (в нашем случае BC перпендикулярно AD) независимо от выбора этих двух пар.
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона.
- Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
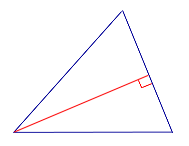
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности (см. рисунок)[1].
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если O{\displaystyle O} — центр описанной окружности △ABC{\displaystyle \triangle ABC}, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}}.
- OH=R2−8R2cosAcosBcosC=9R2−(a2+b2+c2){\displaystyle OH={\sqrt {R^{2}-8R^{2}\cos A\cos B\cos C}}={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}}[2][3]:p. 449, где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника; A,B,C{\displaystyle A,B,C} — внутренние углы треугольника.
- При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью, всегда делится окружностью Эйлера пополам. Это следует из того, что ортоцентр есть центр гомотетии этих двух окружностей с коэффициентом 1/2{\displaystyle 1/2}.
- Четыре попарно пересекающиеся прямые, никакие три из которых не проходят через одну точку (четырёхсторонник), при пересечении образуют четыре треугольника. Их ортоцентры лежат на одной прямой (на прямой Обера).
- Если считать, что ортоцентр треугольника делит первую высоту на части длиной: u и v, вторую высоту на части длиной: w и x, третью высоту на части длиной: y и z, тогда uv = wx = yz[4][5].
- Цепочка уравнений в последнем пункте: uv = wx = yz,- по сути означает, что три пары отрезков, на которые ортоцентр разделяет три высоты остроугольного треугольника, подчиняются правилу хорд, пересекающихся внутри окружности, например: uv = wx. Отсюда автоматически следует то, что через четыре конца любых двух высот остроугольного треугольника всегда можно провести окружность (высоты в ней будут пересекающимися хордами). Оказывается, это утверждение сохраняет силу и для тупоугольного, и прямоугольного треугольников.
- Расстояние от стороны до центра описанной окружности равно половине расстояния от противоположной ей вершины до ортоцентра[6][7].
- Сумма квадратов расстояний от вершин до ортоцентра плюс сумма квадратов сторон равна двенадцати квадратам радиуса описанной окружности[8].
- Три основания высот остроугольного треугольника или три проекции ортоцентра на стороны треугольника образуют ортотреугольник.
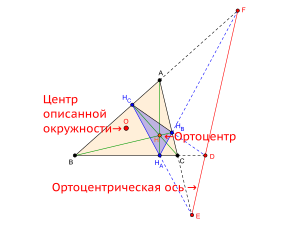 Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра
Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра- Трилинейной полярой ортоцентра является ортоцентрическая ось DEF (Orthic axis) (см. рис.)
- R+r=ka+kb+kc=12(dA+dB+dC),{\displaystyle R+r=k_{a}+k_{b}+k_{c}={\frac {1}{2}}(d_{A}+d_{B}+d_{C}),}
где ka,kb,kc{\displaystyle k_{a},k_{b},k_{c}} — расстояния от центра описанной окружности соответственно до сторон a,b,c{\displaystyle a,b,c} треугольника, dA,dB,dC{\displaystyle d_{A},d_{B},d_{C}} — расстояния от ортоцентра соответственно до вершин A,B,C{\displaystyle A,B,C} треугольника.
Расстояние от центра описанной окружности до стороны a{\displaystyle a}равно:
- ka=a2tgA;{\displaystyle k_{a}={\frac {a}{2\,\mathrm {tg} \,A}};}
расстояние от ортоцентра до вершины A{\displaystyle A} равно:
- dA=atgA.{\displaystyle d_{A}={\frac {a}{\mathrm {tg} \,A}}.}
- ↑ Honsberger, 1995, p. 18.
- ↑ Marie-Nicole Gras, «Distances between the circumcenter of the extouch triangle and the classical centers», Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html
- ↑ Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
- ↑ Altshiller-Court, 2007, p. 94.
- ↑ Honsberger, 1995, p. 20.
- ↑ Altshiller-Court, 2007, p. 99.
- ↑ Honsberger, 1995, p. 17, 23.
- ↑ Altshiller-Court, 2007, p. 102.
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. задача на с. 120—125. параграф 57, с.73.
Ортоцентр – это… Что такое Ортоцентр?
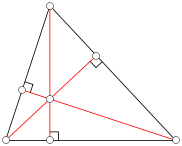
Ортоцентр (от греч. ορθοξ — прямой) — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).
Свойства
- Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если О — центр описанной окружности ΔABC, то ,
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
История
Первое строгое доказательство того, что высоты треугольника пересекаются в одной точке дал Карл Фридрих Гаусс только в XVIII веке
[источник не указан 845 дней].См. также
Литература
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 37-39. — ISBN 5-94057-170-0
Ссылки
Ортоцентр треугольника: полезные факты.
Ортоцентр треугольника: полезные факты
В этой статье доказываются некоторые факты, касающиеся точки пересечения высот треугольника (ортоцентра треугольника), которые могут быть весьма полезны при решении задач.
Пусть  – точка пересечения высот треугольника
– точка пересечения высот треугольника  ,
, 
Тогда:
1) радиусы окружностей, описанных около треугольников  ,
,  ,
,  и
и  равны;
равны;
2) расстояние от вершины 
 вдвое больше расстояния от центра описанной окружности до стороны
вдвое больше расстояния от центра описанной окружности до стороны  ;
;3) расстояние между серединами отрезков  и
и 
 ;
;4)  ;
;
5) точки, симметричные точке  относительно прямой
относительно прямой  и относительно середины стороны
и относительно середины стороны 
 .
.Доказательство.
1) Радиусы окружностей, описанных около треугольников  ,
,  ,
,  и
и 

Радиус окружности, описанной около треугольника можно найти по формуле:

, где  – произвольная сторона треугольника, а
– произвольная сторона треугольника, а  – величина противолежащего угла.
– величина противолежащего угла.
Для треугольника  радиус описанной окружности
радиус описанной окружности 
Рассмотрим четырехугольник  :
:  по свойству вертикальных углов.
по свойству вертикальных углов. 
Тогда для треугольника  радиус описанной окружности
радиус описанной окружности  , то есть равен радиусу описанной окружности треугольника
, то есть равен радиусу описанной окружности треугольника  .
.
2) Расстояние от вершины  до точки
до точки  вдвое больше расстояния от центра описанной окружности до стороны
вдвое больше расстояния от центра описанной окружности до стороны  .
.

Докажем, что  , где
, где  – центр описанной окружности, а
– центр описанной окружности, а  – основание серединного перпендикуляра, опущенного из точки
– основание серединного перпендикуляра, опущенного из точки  на сторону
на сторону  . (Вспомним, что центр описанной окружности лежит в точке пересечения серединных перпендикуляров.)
. (Вспомним, что центр описанной окружности лежит в точке пересечения серединных перпендикуляров.)
Пусть точка  симметрична точке
симметрична точке  относительно отрезка
относительно отрезка  .
.
Рассмотрим треугольник  .
. 
Из соображений симметрии  , следовательно,
, следовательно,  .
.
Так как расстояние от точки  до точек
до точек  и
и  равно радиусу окружности, описанной около треугольника
равно радиусу окружности, описанной около треугольника  , и мы только что доказали, что радиус окружности, описанной около треугольника
, и мы только что доказали, что радиус окружности, описанной около треугольника  также равен
также равен  , следовательно, точка
, следовательно, точка  – центр окружности, описанной около треугольника
– центр окружности, описанной около треугольника  , и
, и  .
. 
Проведем окружность с центром в точке  , описанную около треугольника
, описанную около треугольника  :
:
Мы видим, что при параллельном переносе на вектор  окружность с центром в точке
окружность с центром в точке  переходит в окружность c центром в точке
переходит в окружность c центром в точке  , и точка
, и точка  переходит в точку
переходит в точку  , следовательно,
, следовательно,  . Но так как
. Но так как  , получили, что
, получили, что  .
.
Что и требовалось доказать.
3) Расстояние между серединами отрезков  и
и  равно радиусу описанной окружности треугольника
равно радиусу описанной окружности треугольника  .
.
Рассмотрим четырехугольник  .
.
Мы доказали, что  . Кроме того, по доказанному выше,
. Кроме того, по доказанному выше,  . Следовательно, этот четырехугольник – параллелограмм. Точка
. Следовательно, этот четырехугольник – параллелограмм. Точка  – середина отрезка
– середина отрезка  , является также серединой отрезка
, является также серединой отрезка  . Следовательно, отрезок, соединяющий точку
. Следовательно, отрезок, соединяющий точку  с точкой
с точкой  – серединой отрезка
– серединой отрезка  , параллелен отрезкам
, параллелен отрезкам  и
и  и равен им:
и равен им:
 .
.
Что и требовалось доказать.
4) 

Используем доказанные выше факты.
Четырехугольник  – ромб, следовательно, по правилу параллелограмма для сложения векторов получаем
– ромб, следовательно, по правилу параллелограмма для сложения векторов получаем  :
:

Далее, четырехугольник  -параллелограмм, следовательно,
-параллелограмм, следовательно,  .
.
Утверждение доказано.
5) Точки, симметричные точке  относительно прямой
относительно прямой  и относительно середины стороны
и относительно середины стороны  , лежат на описанной окружности треугольника
, лежат на описанной окружности треугольника  .
.
Пусть точка  симметрична точке
симметрична точке  относительно прямой
относительно прямой  :
:

Точка  симметрична точке
симметрична точке  относительно прямой
относительно прямой  . Следовательно, окружность с центром в точке
. Следовательно, окружность с центром в точке  симметрична окуржности с центром в точке
симметрична окуржности с центром в точке  . Точка
. Точка  лежит на окружности с центром в точке
лежит на окружности с центром в точке  (см. п. 2), следовательно, симметричная ей относительно прямой
(см. п. 2), следовательно, симметричная ей относительно прямой  точка
точка  симметричной окружности с центром в точке
симметричной окружности с центром в точке  , то есть описанной около треугольника
, то есть описанной около треугольника  .
.
Пусть точка  симметрична точке
симметрична точке  относительно относительно середины стороны
относительно относительно середины стороны  :
:

Треугольники 
 равны по двум сторонам и углу между ними, следовательно,
равны по двум сторонам и углу между ними, следовательно,  , и точка
, и точка  лежит на окружности, описанной около треугольника
лежит на окружности, описанной около треугольника  .
.
Утверждение доказано.
И. В. Фельдман, репетитор по математике.
8. Ортоцентр треугольника. Ортотреугольник. Свойства ортоцентра треугольника
Ортоцентр — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).
Свойства
Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.
Радиусы окружностей проходящих через любые три точки ортоцентрической системы равны.
Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
Точки, симметричные ортоцентру относительно его сторон, лежат на описанной окружности.
Точки, симметричные ортоцентру относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
Если О — центр
описанной окружности ΔABC, то 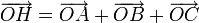 .
.
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Ортотреуго́льник (ортоцентрический треугольник) треугольника ∆ABC — треугольник, вершины которого являются основаниями высот ∆ABC.
Свойства
. Ортоцентрический треугольник остроугольного треугольника АВС обладает наименьшим периметром из всех вписанных треугольников.
Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).
Если точки A1, B1 и C1 на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что
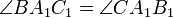 ,
, 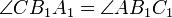 и
и 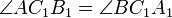 ,
,
то A1B1C1 — ортотреугольник треугольника ABC.
Точки касания вписанной в данный треугольник окружности соединены отрезками, и в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника.
Ортотреугольник отсекает треугольники, подобные данному.
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
Высоты треугольника являются биссектрисами ортотреугольника.
Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .
Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.
9. Вписанные четырехугольники. Вписанные многоугольники
Четырёхугольник, все вершины которого лежат на окружности, называется вписанным.
Сумма противоположных углов вписанного четырёхугольника равна 180°.
Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон (теорема Птолемея).
Площадь S вписанного четырёхугольника со сторонами a, b, c, d можно вычислить по формулам:

 ,где p –
полупериметр, R – радиус окружности.
,где p –
полупериметр, R – радиус окружности.Если a, b, c, d – длины сторон четырёхугольника,
 –
его полупериметр, а α – сумма его противоположных углов, то
площадь S четырёхугольника равна
–
его полупериметр, а α – сумма его противоположных углов, то
площадь S четырёхугольника равна
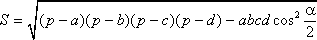 .
.
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид:
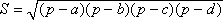 ;это
равенство и называется формулой
Брахмагупты.
Если четырёхугольник имеет и описанную
и вписанную окружности, то формула
становится совсем короткой:
;это
равенство и называется формулой
Брахмагупты.
Если четырёхугольник имеет и описанную
и вписанную окружности, то формула
становится совсем короткой: 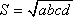 .
.
Если четырехугольник вписан в окружность, то сумма его противоположных углов равна 1800 (свойство вписанных четырехугольников).
1
Действительно, пусть четырехугольник АВСД вписан в окружность (рис.3.61).Тогда сумма
его углов А и С измеряется полусуммой дуг ВСП и ВЛП, составляющих полную окружность, а потому
равна 180°. И Рассмотрим первый случай.
Продолжим тогда сторону ВА за точку А до пересечения с окружностью Р в точке М и проведем хорду МБ (рис.3.63).Четырехугольник ВСБМ вписан в окружность Р. Как доказано, АС+ АМ= 180о.
Но АА >АМ (как внешний угол треугольника БМА), а значит АА+АС>180о.
Получили противоречие. Следовательно,
точка А не может лежать внутри круга, ограниченного
окружностью Р.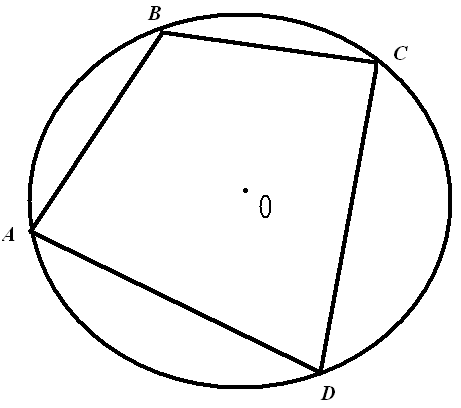
Тэарэма (аб акружнасці, апісанай каля правільнага
многавугольніка). Каля любога правільнага
многавуголь- ніка можна апісаць
акружнасць, і прытым толькі адну.
Дадзена: А 1 А 2А3 ••• Аn —правільны многавугольнік. Даказаць:
існуе пункт, роўнааддалены ад усіх
вяршынь. Ён адзіны. Доказ.
1. Дакажам існаван- не. Няхай О — пункт
перасячэння бісектрыс вуглоў Аг іА2 (рыс. 61). Злучым пункт О адрэзкамі з
астатнімі вяршынямі многаву- гольніка
і дакажам, што ОА1 = ОА2 = … = ОАп.
1) Паколькі
А1 =А2 то 1
= =3,
значыць, трохвугольнік А1А20
раўнабедраны і ОАг = ОА2.
2) Трохвугольнікі А1А20
і А3А2О роўныя па дзвюх стара- нах і вуглу паміж
імі (А1А2 = АзА2,
А2О
— агульная старана і 3
= 4),
значыць, ОА3 = ОАг.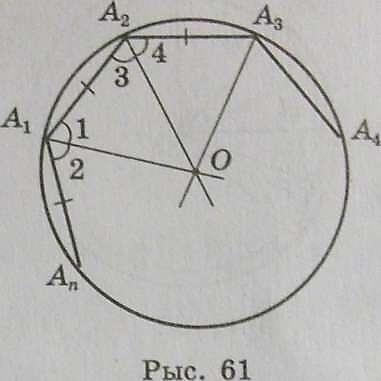
3)Аналагічна можна даказаць, што ОА4 = ОА2, ОА5 = ОА3 і г.д. 4) Такім чынам, ОА1 = ОА2 = … = ОАт, значыць, пункт О роўнааддалены ад усіх вяршынь многавугольніка. Таму акружнасць со (О, ОА1) з’яўляецца апісанай каля многаву- гольніка.
2. Дакажам адзінкавасць. Для гэтага разгледзім якія-не- будзь тры вяршыні многавугольніка, напрыклад, А1 А2, А3. Паколькі праз гэтыя пункты праходзіць толькі адна акруж- насць, то і каля многавугольніка А1, А2, … Аnможна апісаць толькі адну акружнасць.
Ортоцентр — Википедия. Что такое Ортоцентр
Материал из Википедии — свободной энциклопедии
Ортоцентр (от др.-греч. ὀρθός «прямой») — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H{\displaystyle H}. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольном), вне его (в тупоугольном) или совпадать с вершиной (в прямоугольном — совпадает с вершиной при прямом угле). Ортоцентр относятся к замечательным точкам треугольника и перечислен в энциклопедии центров треугольника Кларка Кимберлинга[en] как точка X(4).
Свойства
- Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.
- Более того, при любом разбиении множества ортоцентрической системы точек {A, B, C, D} на две пары, например, {B, C} и {A, D} или при любом другом подобном разбиении, всегда перпендикулярны образующиеся два отрезка прямых с концами в данных точках множеств (в нашем случае BC перпендикулярно AD) независимо от выбора этих двух пар.
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона
- Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности (см. рисунок)[1].
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если O{\displaystyle O} — центр описанной окружности △ABC{\displaystyle \triangle ABC}, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} .
- OH=R2−8R2cosAcosBcosC=9R2−(a2+b2+c2){\displaystyle OH={\sqrt {R^{2}-8R^{2}\cos A\cos B\cos C}}={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}}[2][3]:p. 449, где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника; A,B,C{\displaystyle A,B,C} — внутренние углы треугольника.
- При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью, всегда делится окружностью Эйлера пополам. Это следует из того, что ортоцентр есть центр гомотетии этих двух окружностей с коэффициентом 1/2{\displaystyle 1/2}.
- Четыре попарно пересекающиеся прямые, никакие три из которых не проходят через одну точку (четырёхсторонник), при пересечении образуют четыре треугольника. Их ортоцентры лежат на одной прямой (на прямой Обера).
- Если считать, что ортоцентр треугольника делит первую высоту на части длиной: u и v, вторую высоту на части длиной: w и x, третью высоту на части длиной: y и z, тогда uv = wx = yz[4][5].
- Цепочка уравнений в последнем пункте: uv = wx = yz,- по сути означает, что три пары отрезков, на которые ортоцентр разделяет три высоты остроугольного треугольника, подчиняются правилу хорд, пересекающихся внутри окружности, например: uv = wx. Отсюда автоматически следует то, что через четыре конца любых двух высот остроугольного треугольника всегда можно провести окружность (высоты в ней будут пересекающимися хордами). Оказывается, это утверждение сохраняет силу и для тупоугольного, и прямоугольного треугольников.
- Расстояние от стороны до центра описанной окружности равно половине расстояния от противоположной ей вершины до ортоцентра[6][7].
- Сумма квадратов расстояний от вершин до ортоцентра плюс сумма квадратов сторон равна двенадцати квадратам радиуса описанной окружности[8].
- Три основания высот остроугольного треугольника или три проекции ортоцентра на стороны треугольника образуют ортотреугольник.
 Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра
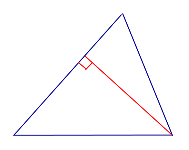
Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра- Трилинейной полярой ортоцентра является ортоцентрическая ось DEF (Orthic axis) (см. рис.)
- R+r=ka+kb+kc=12(dA+dB+dC),{\displaystyle R+r=k_{a}+k_{b}+k_{c}={\frac {1}{2}}(d_{A}+d_{B}+d_{C}),}
где ka,kb,kc{\displaystyle k_{a},k_{b},k_{c}} — расстояния от центра описанной окружности соответственно до сторон a,b,c{\displaystyle a,b,c} треугольника, dA,dB,dC{\displaystyle d_{A},d_{B},d_{C}} — расстояния от ортоцентра соответственно до вершин A,B,C{\displaystyle A,B,C} треугольника.
Расстояние от центра описанной окружности до стороны a{\displaystyle a}равно:
- ka=a2tgA;{\displaystyle k_{a}={\frac {a}{2\,\mathrm {tg} \,A}};}
расстояние от ортоцентра до вершины A{\displaystyle A} равно:
- dA=atgA.{\displaystyle d_{A}={\frac {a}{\mathrm {tg} \,A}}.}
См. также
Примечания
- ↑ Honsberger, 1995, p. 18.
- ↑ Marie-Nicole Gras, «Distances between the circumcenter of the extouch triangle and the classical centers», Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html
- ↑ Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
- ↑ Altshiller-Court, 2007, p. 94.
- ↑ Honsberger, 1995, p. 20.
- ↑ Altshiller-Court, 2007, p. 99.
- ↑ Honsberger, 1995, p. 17, 23.
- ↑ Altshiller-Court, 2007, p. 102.
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. задача на с. 120—125. параграф 57, с.73.
Литература
Ссылки
Ортоцентр — Википедия
Материал из Википедии — свободной энциклопедии
Ортоцентр (от др.-греч. ὀρθός «прямой») — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H{\displaystyle H}. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольном), вне его (в тупоугольном) или совпадать с вершиной (в прямоугольном — совпадает с вершиной при прямом угле). Ортоцентр относятся к замечательным точкам треугольника и перечислен в энциклопедии центров треугольника Кларка Кимберлинга[en] как точка X(4).
Свойства
- Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками. Такую четвёрку иногда называют ортоцентрической системой точек.
- Более того, при любом разбиении множества ортоцентрической системы точек {A, B, C, D} на две пары, например, {B, C} и {A, D} или при любом другом подобном разбиении, всегда перпендикулярны образующиеся два отрезка прямых с концами в данных точках множеств (в нашем случае BC перпендикулярно AD) независимо от выбора этих двух пар.
- Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны (следствие теоремы Гамильтона для окружности Эйлера). Их часто называют окружностями Джонсона
- Последнее утверждение можно сформулировать так: Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих равные радиусы описанных окружностей (следствие теоремы Гамильтона для окружности Эйлера). При этом одинаковый радиус этих трех окружностей равен радиусу окружности, описанной около исходного остроугольного треугольника.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности (см. рисунок)[1].
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если O{\displaystyle O} — центр описанной окружности △ABC{\displaystyle \triangle ABC}, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} .
- OH=R2−8R2cosAcosBcosC=9R2−(a2+b2+c2){\displaystyle OH={\sqrt {R^{2}-8R^{2}\cos A\cos B\cos C}}={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}}[2][3]:p. 449, где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника; A,B,C{\displaystyle A,B,C} — внутренние углы треугольника.
- При изогональном сопряжении ортоцентр переходит в центр описанной окружности.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью, всегда делится окружностью Эйлера пополам. Это следует из того, что ортоцентр есть центр гомотетии этих двух окружностей с коэффициентом 1/2{\displaystyle 1/2}.
- Четыре попарно пересекающиеся прямые, никакие три из которых не проходят через одну точку (четырёхсторонник), при пересечении образуют четыре треугольника. Их ортоцентры лежат на одной прямой (на прямой Обера).
- Если считать, что ортоцентр треугольника делит первую высоту на части длиной: u и v, вторую высоту на части длиной: w и x, третью высоту на части длиной: y и z, тогда uv = wx = yz[4][5].
- Цепочка уравнений в последнем пункте: uv = wx = yz,- по сути означает, что три пары отрезков, на которые ортоцентр разделяет три высоты остроугольного треугольника, подчиняются правилу хорд, пересекающихся внутри окружности, например: uv = wx. Отсюда автоматически следует то, что через четыре конца любых двух высот остроугольного треугольника всегда можно провести окружность (высоты в ней будут пересекающимися хордами). Оказывается, это утверждение сохраняет силу и для тупоугольного, и прямоугольного треугольников.
- Расстояние от стороны до центра описанной окружности равно половине расстояния от противоположной ей вершины до ортоцентра[6][7].
- Сумма квадратов расстояний от вершин до ортоцентра плюс сумма квадратов сторон равна двенадцати квадратам радиуса описанной окружности[8].
- Три основания высот остроугольного треугольника или три проекции ортоцентра на стороны треугольника образуют ортотреугольник.
- Трилинейной полярой ортоцентра является ортоцентрическая ось DEF (Orthic axis) (см. рис.)
- R+r=ka+kb+kc=12(dA+dB+dC),{\displaystyle R+r=k_{a}+k_{b}+k_{c}={\frac {1}{2}}(d_{A}+d_{B}+d_{C}),}
где ka,kb,kc{\displaystyle k_{a},k_{b},k_{c}} — расстояния от центра описанной окружности соответственно до сторон a,b,c{\displaystyle a,b,c} треугольника, dA,dB,dC{\displaystyle d_{A},d_{B},d_{C}} — расстояния от ортоцентра соответственно до вершин A,B,C{\displaystyle A,B,C} треугольника.
Расстояние от центра описанной окружности до стороны a{\displaystyle a}равно:
- ka=a2tgA;{\displaystyle k_{a}={\frac {a}{2\,\mathrm {tg} \,A}};}
расстояние от ортоцентра до вершины A{\displaystyle A} равно:
- dA=atgA.{\displaystyle d_{A}={\frac {a}{\mathrm {tg} \,A}}.}
См. также
Примечания
- ↑ Honsberger, 1995, p. 18.
- ↑ Marie-Nicole Gras, «Distances between the circumcenter of the extouch triangle and the classical centers», Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html
- ↑ Smith, Geoff, and Leversha, Gerry, «Euler and triangle geometry», Mathematical Gazette 91, November 2007, 436—452.
- ↑ Altshiller-Court, 2007, p. 94.
- ↑ Honsberger, 1995, p. 20.
- ↑ Altshiller-Court, 2007, p. 99.
- ↑ Honsberger, 1995, p. 17, 23.
- ↑ Altshiller-Court, 2007, p. 102.
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. задача на с. 120—125. параграф 57, с.73.
Литература
Ссылки
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике – Планиметрия
Высота треугольника. Свойство высоты прямоугольного треугольника
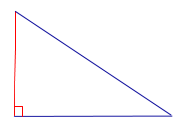
Определение 1. Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
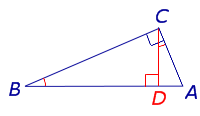
Рис.1
На рисунке 1 изображена высота BD, проведённая из вершины B треугольника ABC. Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
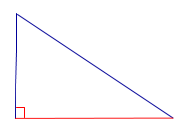
Утверждение. Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
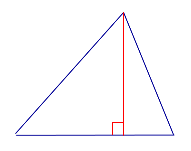
Рис.2
Доказательство. Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
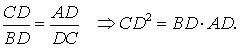
В силу признака подобия прямоугольных треугольников треугольники BCD и ACD подобны. Следовательно,
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD, что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Расположение высот у треугольников различных типов
| Остроугольный треугольник |
Все высоты остроугольного треугольника лежат внутри треугольника. |
| Прямоугольный треугольник |
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
| Тупоугольный треугольник |
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
Ортоцентр треугольника
Теорема 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
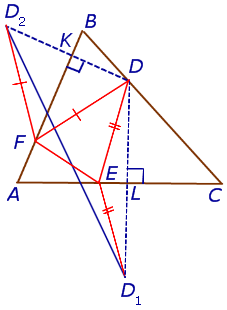
Рис.3
Обозначим точки пересечения этих прямых символами A1, B1 и C1, как показано на рисунке 3.
В силу параллельности прямых AC и C1A1, а также BC и C1B1 четырёхугольники AC1BC и ABA1C – параллелограммыпараллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства
C1B = AC = BA1.
Следовательно, точка B является серединой стороны C1A1.
В силу параллельности прямых BC и C1B1, а также AB и B1A1 четырёхугольники AC1BC и ABCB1 – параллелограммы,параллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства
C1A = BC = A1B1.
Следовательно, точка A является серединой стороны C1B1.
В силу параллельности прямых AB и B1A1, а также AC и C1A1 четырёхугольники ABA1C и ABCB1 – параллелограммыпараллелограммы, откуда вытекают равенствавытекают равенствавытекают равенства
A1C = AB = B1C.
Следовательно, точка C является серединой стороны B1A1.
Таким образом, высоты треугольника ABC являются серединными перпендикулярами треугольника A1B1C1 (рис. 4),
Рис.4
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Расположение ортоцентров у треугольников различных типов
| Фигура | Рисунок | Описание |
| Остроугольный треугольник | Ортоцентр остроугольного треугольника лежит внутри треугольника. | |
| Прямоугольный треугольник | Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла | |
| Тупоугольный треугольник | Ортоцентр тупоугольного треугольника лежит вне треугольника. |
Ортоцентрический треугольник
Решим следующую задачу.
Задача. В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC.
Рис.5
Решение. Рассмотрим треугольники ADC и BEC. Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
Из подобия треугольников ABC и EDC (рис.5) вытекает важное следствие.
Следствие 1.
Определение 3. Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
Рис.6
Из определения 3 и следствия 1 вытекает следствие 2.
Следствие 2. Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
Рис.7
Тогда справедливы равенства
Из следствия 2 вытекает теорема 2.
Теорема 2. Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
Доказательство. Воспользовавшись следствием 2, получаем:
что и требовалось доказать.
Задача Фаньяно
Задача Фаньяно. Рассматриваются всевозможные треугольники DEF, вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC.
Решение. Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D1 точку, симметричную точке D относительно прямой AC, и обозначим символом D2 точку, симметричную точке D относительно прямой AB (рис.8).
Рис.8
Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D1D2. Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF, вершины F и E которого являются точками пересечения прямой D1D2 с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D1D2 (рис.9).
Рис.9
Заметим также, что выполнено равенство
AD = AD1 = AD2.
Кроме того, выполнено равенство
Поэтому
Отсюда вытекает, что длина отрезка D1D2 будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC. Другими словами, наименьшим периметром обладает такой треугольник DEF, у которого вершина D является основанием высоты треугольника ABC, проведённой из вершины A, а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.
Если обозначить длину высоты, проведённой из вершины A, длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:
Следовательно, наименьший периметр рассматриваемых треугольников DEF равен
Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.
Лемма. Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).
Рис.10
В этом случае отрезок D1D2 проходит через точки F и E.
Доказательство. Заметим, что в силу следствия 2 выполняются равенства:
Кроме того, в силу равенства треугольников DFK и KFD2, а также в силу равенства треугольников DEL и LED1 выполняются равенства:
Следовательно,
откуда вытекает, что углы AEF и D1EL , а также AFE и D2FK являются вертикальными углами. Это означает, что точки D1, F, E, D2 лежат на одной прямой. Лемма доказана.
Доказательство леммы и завершает решение задачи Фаньяно.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.


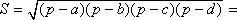
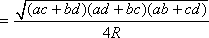 ,где p –
полупериметр, R – радиус окружности.
,где p –
полупериметр, R – радиус окружности.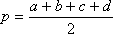 –
его полупериметр, а α – сумма его противоположных углов, то
площадь S четырёхугольника равна
–
его полупериметр, а α – сумма его противоположных углов, то
площадь S четырёхугольника равна